People in Space - Who Are They?

Report

Author

Spelling Bees 🐝🍯

Introduction

Space is one of the most fascinating new frontiers of human exploration, and new explorations are being made every day. After we stumbled upon this comprehensive astronaut-centered dataset from Tidy Tuesday, we sought to investigate and better understand any underlying relationships between the personal attributes of an astronaut and the amount of time they’ve spent on space missions.

Research Question: How do certain professional and personal attributes affect the amount of time an astronaut spends on space missions?

Goal of Project: We seek to analyze how an astronaut’s particular qualities and attributes, including age, nationality, sex, and military-civilian status, may influence the time an astronaut has spent on missions. Through this analysis, we hope to show how certain qualities may or may not influence one’s career experience as an astronaut. In this case, we are using an astronaut’s total mission hours as an indicator of their career experience. Moreover, we hope to potentially reveal any bias in which mission length is more strongly correlated with a particular military status, nationality, or sex. We hope that our analysis will benefit aspiring astronauts.

Data: The dataset we used was compiled by Tom Mock, a member of the Tidy Tuesday community. Contributors of the data include Tatsuya Corlett, Mariya Stavnichuk, and Georgios Karamanis, who collected the data from NASA, Roscosmos, and other websites. It records all instances of astronauts who have publically participated in space missions between 1961 and 2019. There are 1,277 observations with 24 variables. In the context of our research question, we chose to focus on the relationship between the variables total_hrs_sum (total hours spent on missions), military_civilian status, year_of_birth, sex, and nationality.

Reading and Cleaning Data

Rows: 1277 Columns: 24
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (11): name, original_name, sex, nationality, military_civilian, selectio...
dbl (13): id, number, nationwide_number, year_of_birth, year_of_selection, m...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

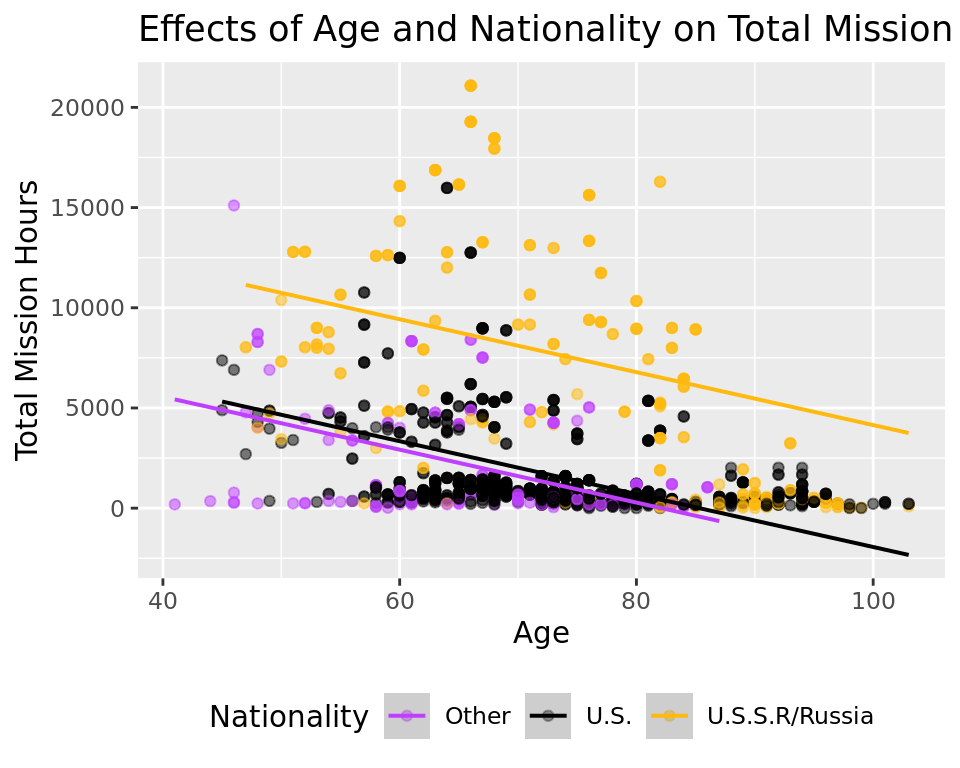
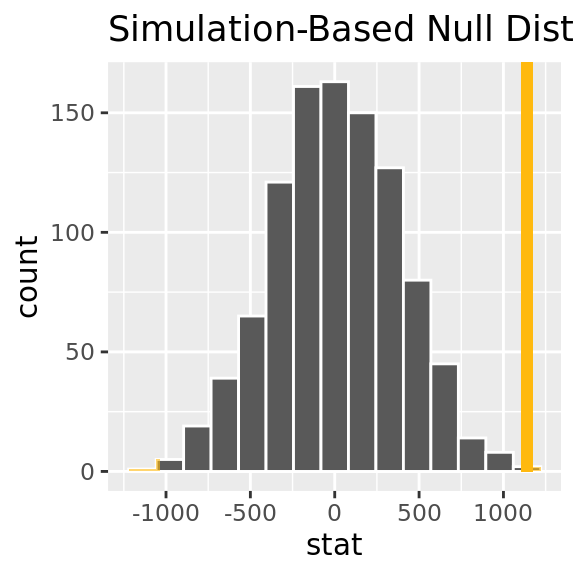
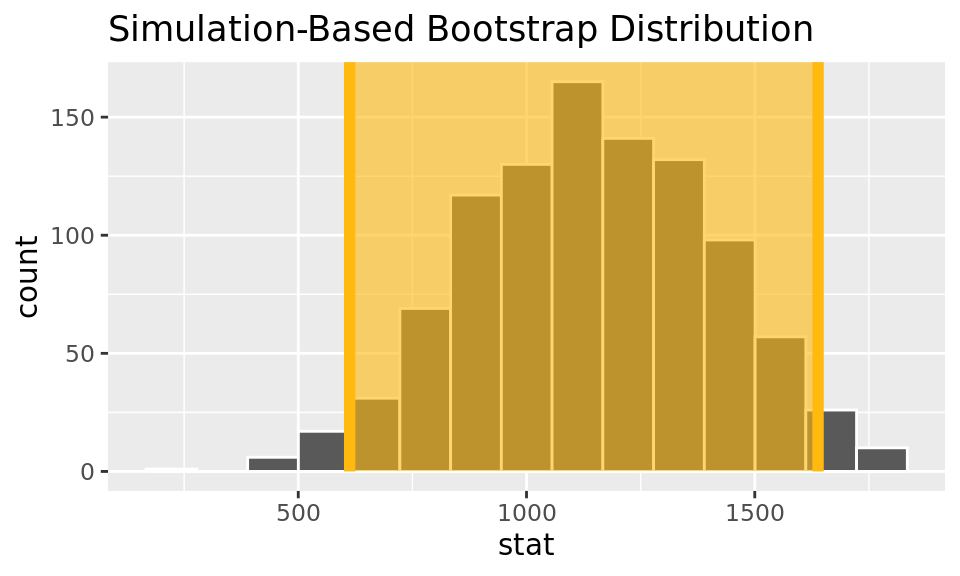
Rows: 1,277
Columns: 24
$ id                       <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14…
$ number                   <dbl> 1, 2, 3, 3, 4, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, …
$ nationwide_number        <dbl> 1, 2, 1, 1, 2, 2, 2, 4, 4, 3, 3, 3, 4, 4, 5, …
$ name                     <chr> "Gagarin, Yuri", "Titov, Gherman", "Glenn, Jo…
$ original_name            <chr> "ГАГАРИН Юрий Алексеевич", "ТИТОВ Герман Степ…
$ sex                      <chr> "male", "male", "male", "male", "male", "male…
$ year_of_birth            <dbl> 1934, 1935, 1921, 1921, 1925, 1929, 1929, 193…
$ nationality              <chr> "U.S.S.R/Russia", "U.S.S.R/Russia", "U.S.", "…
$ military_civilian        <chr> "military", "military", "military", "military…
$ selection                <chr> "TsPK-1", "TsPK-1", "NASA Astronaut Group 1",…
$ year_of_selection        <dbl> 1960, 1960, 1959, 1959, 1959, 1960, 1960, 196…
$ mission_number           <dbl> 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 3, 1, 2, 1, …
$ total_number_of_missions <dbl> 1, 1, 2, 2, 1, 2, 2, 2, 2, 3, 3, 3, 2, 2, 3, …
$ occupation               <chr> "pilot", "pilot", "pilot", "PSP", "Pilot", "p…
$ year_of_mission          <dbl> 1961, 1961, 1962, 1998, 1962, 1962, 1970, 196…
$ mission_title            <chr> "Vostok 1", "Vostok 2", "MA-6", "STS-95", "Me…
$ ascend_shuttle           <chr> "Vostok 1", "Vostok 2", "MA-6", "STS-95", "Me…
$ in_orbit                 <chr> "Vostok 2", "Vostok 2", "MA-6", "STS-95", "Me…
$ descend_shuttle          <chr> "Vostok 3", "Vostok 2", "MA-6", "STS-95", "Me…
$ hours_mission            <dbl> 1.77, 25.00, 5.00, 213.00, 5.00, 94.00, 424.0…
$ total_hrs_sum            <dbl> 1.77, 25.30, 218.00, 218.00, 5.00, 519.33, 51…
$ field21                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ eva_hrs_mission          <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.0…
$ total_eva_hrs            <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.0…

To make our analysis process easier, we adjusted the dataframe to include an age variable based on the year_of_birth variable to help us conduct more relevant analyses. In addition, we altered nationality categories to U.S.S.R/Russia, U.S., or Other since we are most interested in what are considered “big names” in the space industry. Lastly, we used the military_civilian variable to create a new binary categorical variable, military_binary.

Dictionary for Relevant Variables

Variable Name	Description
`total_hrs_sum`	Total hours an astronaut has spent on space missions
`military_civilian`	Indicates an astronaut’s military status as `military` or `civilian`; converted to `military_binary` for analysis purposes
`military_binary`	Indicates an astronaut’s military as either a `1` (military) or `0` (civilian)
`year_of_birth`	Birth year of astronaut; converted to `age` for analysis purposes
`age`	Age of astronaut, assuming they are still alive today
`sex`	Indicates the sex of an astronaut as either male or female
`nationality`	Indicates the nationality of the astronaut; converted into `nationality_tidied` for analysis purposes
`nationality_tidied`	Indicates the nationality of the astronaut as either `U.S.S.R/Russia`, `U.S.`, or `Other`

Exploratory Data Analysis

Calculating Summary Statistics

To gain a better and more holistic understanding of the data we are using to for our analysis, we first look at the basic summary statistics that describe our data:

# A tibble: 1 × 4
  count_males count_females mean_tot_hrs_sum_male mean_tot_hrs_sum_female
        <int>         <int>                 <dbl>                   <dbl>
1        1134           143                 3096.                   1958.

# A tibble: 1 × 4
  military_proportion median_age mean_age median_total_hours
                <dbl>      <dbl>    <dbl>              <dbl>
1                   0         72     72.3                932

# A tibble: 1 × 5
  mean_total_hours max_total_hours min_total_hours us_ast_count ussr_ast_count
             <dbl>           <dbl>           <dbl>        <int>          <int>
1            2968.          21084.            0.61          861            273

From these summary statistics, we can see that, publicly, there have only been 143 instances of a female astronaut compared to 1,134 instances of a male astronaut on a mission within our dataframe. The mean and median of the ages of astronauts in this dataset both round to 72, signifying a more normal distribution. The same is not true for the mean, 2,968 hours, and median, 932 hours, of the total hours sum, which indicates that there is a skew to the right regarding total mission hours. Finally, we find that there are significantly more U.S. astronaut entries than Russian astronaut entries.

Visualizing Initial Findings

Moving past summary statistics, in this section, we briefly explore some trends in our data which we’ll look into deeper in our analysis.

Using the count function, we are able to determine the number of times an astronaut appears in the astronauts dataset which corresponds to the number of missions they’ve been on. Through this barchart we can see that astronauts are most frequently part of 4 missions or less. Again, we see the difference in frequency between females and males on missions, which we’ll take note of as we continue our analysis.

Next, we created a general scatterplot of the total hours sum versus age and facet wrapping by sex. From this visualization, there appears to be a general negative relationship between age and total mission hours, with these averages appearing higher for males. However, this is something that should be investigated in the future to test whether these differences are statistically significant in determining an astronaut’s time in space.

`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'

We can see that Russia has the highest average total_hrs_sum in this dataset at over 7,000 hours. The U.S average is only a fraction of Russia’s at around 1,500 hours, though earlier we noticed that the number of astronauts from the U.S. are noticeably higher than those from Russia. We will look into this further in our analysis.

Finally, with the density plot below, we can see the distributions of the time our astronauts have spent in space faceted by military status. 0 indicates a civilian status, and 1 a military status. Both groups are right skewed and share a similar trend, signifying that there may not be a relationship between military status and time spent in space. This variable will be explored further in our methodology.

Now that we’ve gotten a better sense of the dataset we’re working with, we’ll move on to using techniques learned in class to make some more concrete conclusions.

Methodology

In this section, we dive into predictive modeling and calculating inferential statistics.

Our analysis process begins with us taking educated guesses at the types of characteristics that might affect an astronaut’s experience in space. We then put these to the test using logistic and linear regression and made conclusions based on our findings. An overview of our models are below:

Logistic Regression | Response: militar_binary | Explanatory: total_hrs_sum
Linear Regression | Response: total_hrs_sum | Explanatory: age, nationality
Linear Regression | Response: total_hrs_sum | Explanatory: sex

To bolster our above findings, we conducted hypothesis testing in conjunction with bootstrapping in order to discern if there is a significant difference between the mean time in space for men versus women. Since we only had a single large sample, utilizing bootstrapping to predict a population parameter from our sample is appropriate. Moreover, hypothesis testing was useful in either disproving or not our null hypothesis. The construction of a 95% confidence interval further supported our findings from our hypothesis testing as it showed the range within what the population parameter would likely be in.

Linear and Logistic Modelling

Logistic model predicting military status from total mission hours

# A tibble: 2 × 5
  term             estimate std.error statistic  p.value
  <chr>               <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    0.435      0.0700        6.22  5.08e-10
2 total_hrs_sum -0.00000690 0.0000135    -0.511 6.09e- 1

\[ log(p/1-p) = 0.435 - 0.00000699 \times total\_hrs\_sum \]

The probability \(p\) that an astronaut is of military status (success) given the total number of hours they’ve spent in space is denoted by: \(p = e^{(0.435 - 0.00000699x)} /(1+ e^{(0.435 -0.00000699x)})\). From our logistic model, we observed that for each 1 hours increase in total_hrs_sum, the likelihood of them being of military status decreases by a factor of 0.00000699. We can see that there isn’t a significant indication, or at best, a very small but negligible, indication of military status’ potential to predict the total number of hours an astronaut has spent in space. So we can conclude this attribute is not strongly correlated with the amount of time an astronaut will dedicate to missions.

Linear Model Predicting Hours Spent in Space from Age and Nationality

# A tibble: 4 × 5
  term                             estimate std.error statistic  p.value
  <chr>                               <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)                        10837.    584.       18.5  3.63e-68
2 age                                 -132.      7.84    -16.8  1.48e-57
3 nationality_tidiedU.S.               421.    288.        1.46 1.44e- 1
4 nationality_tidiedU.S.S.R/Russia    6506.    330.       19.7  1.34e-75

For this linear model, we chose to create an additive model, rather than an interactive model. Not only are the additive and interactive model’s adjusted r squared values very similar (0.45 vs. 0.44), but the principle of Occam’s Razor states that the most simple model is ideal. Thus, we chose the simpler additive model over the interactive model since both models have similar accuracy.
Ultimately, the additive effect allows us to observe and model the rate of change of the total number of hours spent in space by an astronaut as age increases across different nationalities without assuming any interaction between age and nationality.

`geom_smooth()` using formula = 'y ~ x'

\[ \widehat{total hours} = 10837.30 - 131.97 \times age + 420.78 \times U.S. + 6506.22 \times Russia \]

All else held constant, for every 1 year increase in age, we expect the corresponding total hours spent in space by an astronaut of this new age group to be lower, on average, by 131.97 hours.

Astronauts of age 0 coming from a nationality other than the U.S. or Russia are expected, on average, to have spent 10,837.3 hours in space. Astronauts of age 0 with a U.S. nationality are expected, on average, to have spent 11,258.08 hours in space. Astronauts of age 0 with a U.S.S.R. nationality are expected, on average, to have spent 17,342.52 hours in space. However, an astronaut aged 0 is impossible, so the intercept is not meaningful in this context.

On average, regardless of age, an astronaut of U.S. nationality will have spent 420.78 hours more in space than an astronaut from a non-U.S. and non-U.S.S.R. nationality, while an astronaut of U.S.S.R. nationality will spend an average of 6,506.22 hours more in space than an astronaut from a non-U.S. and non-U.S.S.R. nationality.

R² Value of Model

[1] 0.4431108

The R-squared value is the percentage of variability in total hours spent in space explained by the linear relationship with age. In this case, around 44.31% of the variability in total hours can be explained by the linear relationship with age. This indicates that this model is not extremely nor weak.

With this linear regression model and r-squared value, we can conclude that age is a moderately strong predictor of the amount of time an astronaut has spent in space, with astronauts of a Russian nationality following this same downward trend, but holding higher averages of total hours spent in space when put in comparison to astronauts of other nationalities.

Linear Model Predicting Time Spent in Space from Sex

# A tibble: 2 × 5
  term        estimate std.error statistic      p.value
  <chr>          <dbl>     <dbl>     <dbl>        <dbl>
1 (Intercept)    1958.      351.      5.57 0.0000000305
2 sexmale        1138.      373.      3.05 0.00232

\[ \widehat{time\_in\_space\_female} = 1957.80 + 1137.97\times male \]

The predicted average time spent in space for a female is 1,957.80 hours. On the other hand, the predicted average time spent in space for a male 1,137.97 hours greater than females, or 3,095.77 hours.

Hypothesis Testing and Bootstrapping

In this section, we explore the difference in the average total mission times between male and female astronauts.

Null hypothesis: The mean time spent in space by male astronauts is equal to the mean time spent in space by female astronauts.

Alternative Hypothesis: There is a difference in the mean time spent in space between male and female astronauts.

Calculating and Visualizing p-value

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.002

Results

With a p-value of 0.002, which is smaller than the discernibility level of 0.05, we reject the null hypothesis. The data provide convincing evidence that there is a difference between the mean total number of hours that female astronauts have spent in space compared to that of male astronauts.

In context, the probability of observing a difference in sample means of total number of hours spent in space between 143 female and 1,134 male astronauts of 1,137.971 hours or more, in either direction, is 0.002 if in fact the two population proportions are equal. This being very low signifies that this data shows that there is a high likelihood of a difference in mean total hours amongst the personal attribute of sex.

Visualizing a Bootstrap of Data

First we calculate the lower and upper bounds of the confidence interval before visualizing the distribution.

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     613.    1639.

Based on the distribution above, we are 95% confident that the mean total number of hours that female astronauts have spent on missions is 612.6 to 1,638.6 hours less than the number of hours male astronauts have spent on missions. This significant difference between these two sexes may then underly in the historical prominence of men being permitted in space more than women. Not only were women in space a few years after men, they were also more of a scarcity as observed in the higher skew to the right in age for female astronauts (younger on average) than males as found in our summarry statistics.

Discussion

Based on our analysis of the data, we are able to make certain conclusions as well as recommendations for future exploration. Firstly, since our logistic model had an extremely small slope, we found that military status is not a strong predictor of total mission hours, which we had not expected. Secondly, we found a statistically significant difference in averages in time spent in space between males and females. Thirdly, we found a negative relationship between age and total mission hours which implies younger astronauts are getting more field experience than older ones. Finally, we found a significant relationship between total mission hours and nationality, with Russia having a statistically higher average in hours followed by the U.S. and then other nations.

However, there are several limitations in our analysis. Firstly, the number of observations for females in the data is significantly smaller than for males. Thus, comparing statistics between the two presenting a potential bias in our interepretation of the observed differences in mean total time. Additionally, since the mean is not a robust statistic, it is prone to significant shifts if outliers are present, especially in smaller samples. For the future, we recommend comparing the medians instead between the sexes to decrease the possibility of shifts due to outliers.

Moreover, our additive model had an adjusted r-squared value of 0.4431. While this is not a terribly low value, it is not extremely high either, showing that this model is not extremely effective. For future analysis, we recommend finding a different combination of predictor variables, or incorporating new, relevant predictor variables altogether, to potentially increase the adjusted r-squared value for our linear regression model.

Since we share an interest in job discrimination, future work should seek to analyze the potential presence of any bias associated with sex or nationality. Specifically, models could be fitted and hypothesis testing could be employed to analyze whether certain countries favor having more male astronauts than female astronauts. Moreover, further analysis of the data could explore a subset of the data beginning from when females started prominently being part of space missions and the effects of that on the total mission hours of that demographic. This could be executed through predicting time in space through the interaction of age and sex.